GABARITO PRF: RLM – Confira os comentários
GABARITO PRF 2019: Gabarito e correção prova de RLM
Olá, alfartanos! A prova do concurso PRF foi realizada neste domingo, dia 03 de fevereiro de 2019. Nossa equipe de professores reuniram-se para fazer os comentários das provas. Confira, nesta postagem, o GABARITO PRF 2019: Gabarito e correção prova de RLM.
GABARITO PRF: Comentários de RLM
Numeração da questão / Disciplina / Início da Questão / Gabarito
| 21 | Raciocínio Lógico-Matemático | Se an for o n-ésimo termo da sequencia, | Certo |
| 22 | Raciocínio Lógico-Matemático | O padrão apresentado pela referida sequê | Errado |
| 23 | Raciocínio Lógico-Matemático | A partir do padrão da sequência, infere- | Errado |
| 24 | Raciocínio Lógico-Matemático | figura ilustrativa | Errado |
| 25 | Raciocínio Lógico-Matemático | figura ilustrativa | Certo |
| 26 | Raciocínio Lógico-Matemático | figura ilustrativa | Certo |
RLM
21 – CERTO
Comentário: A sequência apresentada obedece exatamente a lei de formação, para n 3, em que an = 2 x an-2.
a3 = 2 x a3-2 = 2 x a1
a4 = 2 x a4-2 = 2 x a2
a5 = 2 x a5-2 = 2 x a3
(25, 75, a3, a4, a5, …)
Substituindo pela lei de formação an = 2 x an-2, temos que:
a3 = 2 x a3-2 = 2 x a1 = 2 x 25 = 50
a4 = 2 x a4-2 = 2 x a2 = 2 x 75 = 150
a5 = 2 x a5-2 = 2 x a3 = 2 x 50 = 100
(25, 75, 50, 150, 100, …)
22 – ERRADO
Comentário: Os valores apresentados, (25, 75, 50, 150, 100,…), nesta ordem, não podem corresponder a ordenadas de pontos do gráfico de uma função afim de inclinação positiva, pois não estão em ordem crescente.
23 – ERRADO
Comentário: Para encontrar o 12º valor, vamos substituir (n=12), na lei de formação
an = 2 x an-2. Logo,
a12 = 2 x a12-2
a12 = 2 x a10
a12 = 2 x 1200
a12 = 2400
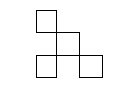
24 – ERRADO
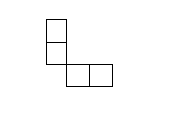
Comentário: A figura da questão não representa à possibilidade de representar uma vista superior da figura do enunciado.
Vejamos a justificativa:
Os blocos dispostos no centro da figura, para atender a vista da esquerda, teriam que possui 2 blocos de altura, o que contrariariam a vista frontal.
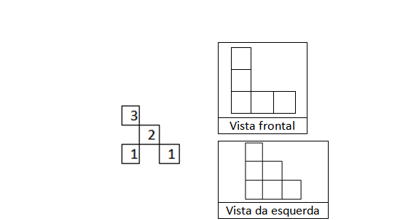
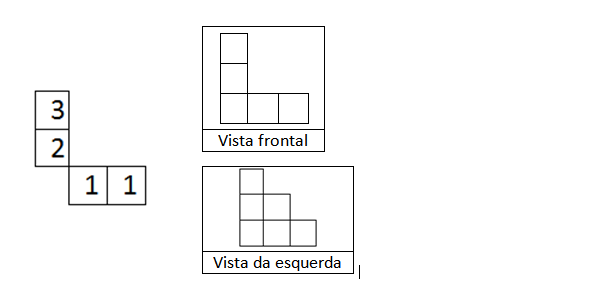
25 – CERTO
Comentário: A figura da questão representa à possibilidade de representar uma vista superior da figura do enunciado.
Vejamos a justificativa: Os blocos dispostos poderiam obter a seguintes quantidades:
Observamos que atende por completo a vista frontal e a vista da esquerda.
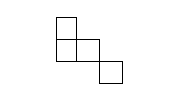
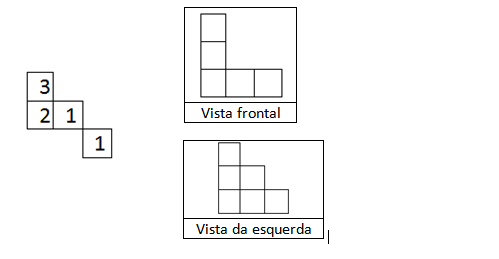
26 – CERTO
Comentário: A figura da questão representa à possibilidade de representar uma vista superior da figura do enunciado.
Vejamos a justificativa: Observamos que atende por completo a vista frontal e a vista da esquerda.
Observamos que atende por completo a vista frontal e a vista da esquerda.
27 – CERTO
Comentário: De acordo com o modelo dado pela função f(x) = 350 + 150 .e-x, no final do primeiro ano (x=1), temos que:
f(x) = 350 + 150 .e-x
f(1) = 350 + 150 .e-1
f(1) = 350 + 150.(1/e)
Substituindo e (constante de Euler) por e = 2,7 (aproximadamente), ficamos com:
f(1) = 350 + 150.(1/2,7)
f(1) = 350 + 55,55…
f(1) = 405,55…
28 – ERRADO
Comentário: De acordo com o modelo dado pela função f(x) = 350 + 150 .e-x, após 10 anos (x>10), temos que:
Vamos encontrar o valor de f(10) e comparar para x=11, x=12, …
Para x=10
f(x) = 350 + 150 .e-x
f(10) = 350 + 150.e-10
f(10) = 350 + 150.(1/e10)
Substituindo e (constante de Euler), por e = 2,7 (aproximadamente), ficamos com:
f(10) = 350 + 150.(1/2,710)
Observa-se que o valor de 150.(1/2,710), resultará em um valor inferior a 1, logo f(10) > 350.
>> Confira a correção ao vivo clicando aqui <<